A Hallmark of Topological Insulators is Measured in Atoms

Q.-X. Lv et al. [1]

Materials that exist in a quantum spin Hall state have a bulk that behaves like an insulator and a surface that segregates electrons according to their spin. Researchers have developed experimental condensed-matter models for such “topological” insulators. But measuring the parameter (the so-called spin Chern number) that quantifies the surface segregation of the spins remains difficult. Now Qing-Xian Lv of South China Normal University and his colleagues have measured the spin Chern number in a gas of ultracold atoms [1].

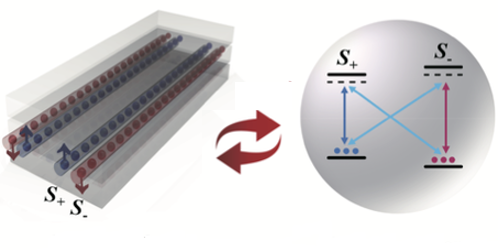
Lv and his colleagues studied the so-called Bernevig-Hughes-Zhang (BHZ) model. In that model, a rectangularly shaped system is divided up into four channels that run parallel to the long edges of the rectangle. The two outer channels carry electrons whose spins point down, while the inner channels carry electrons whose spins points up. This arrangement gives the system chiral edge states, as electrons with opposite spins move in opposite directions when viewed from the short edge of the rectangle.

In their experiments, Lv and his colleagues used atoms instead of electrons. In this system the electronic bands are replaced by the four energy levels of ultracold rubidium atoms. These levels group together in two pairs, with each pair having a different pseudospin—a form of angular momentum analogous to the spin of an electron.

The team manipulated the two pseudospins and the coupling between pairs using a series of brief microwave pulses. They showed that they could measure a Chern-number-like parameter for the system from the effective magnetic field of each pseudospin.

–Rachel Berkowitz

Rachel Berkowitz is a Corresponding Editor for Physics based in Vancouver, Canada.