Recently, the research team led by Professors Hui Yan and Shi-Liang Zhu at South China Normal University (SCNU) has made significant progress in the field of quantum physics by successfully verifying the “quantum principle of least action” experimentally. Their achievement, titled “Demonstration of the quantum principle of least action with single photons” was published in the prestigious journal Nature Photonics on May 22 (the article website: https://www.nature.com/articles/s41566-023-01212-1).

The Principle of Least Action (PLA) posits that if nature has a purpose, it will follow a minimum or critical path. This principle, along with its variations and generalizations, has numerous applications in physics and serves as a roadmap to appreciating the elegance of physics. Nevertheless, this principle had never been experimentally confirmed at the quantum level until the aforementioned experiment.

The PLA is widely regarded by scientists as the most universal and fundamental principle in physics, even in natural science It has a concise and unified aesthetic characteristic in science and holds an incredibly significant position in both the history of physics and scientific advancement. The ultimate dream of a physicist is to write the secrets of the entire universe on a small piece of paper, and the PLA may be one of the fundamental principles that must be written on the list. The PLA, also known as the Maupertuis principle, is named after one of its founders, the esteemed scientist Maupertuis (1698-1759), who was the first to verbally articulate the PLA. Maupertuis used this principle to derive the laws of reflection and refraction of light, and dedicated his life to proving the universality of this principle. During almost the same time, the renowned mathematician Euler presented the initial mathematical concept of this principle, which ultimately led to the derivation of the variational equation now recognized as the Euler-Lagrange equation. In 1834, mathematician Hamilton consolidated these mathematical concepts into Hamilton’s principle, which paved the way for the legendary applications of the PLA in the fields of mathematics, mechanics, and physics.

In the late 19th century, the renowned physicist Helmholtz applied the PLA to the study of thermodynamics and electrodynamics. Through his work, Helmholtz was able to demonstrate that electrodynamics could be derived from this principle. He went on to assert that the PLA was a fundamental principle that governed the entire field of physics, stating, “a valuable heuristic principle and leitmotif in striving for a formulation of the laws of new classes of phenomena” Since then, a multitude of physicists and mathematicians, including Planck, Noether, Hilbert, Schrödinger, and Feynman, have dedicated themselves tirelessly to the path paved by Helmholtz, yielding fruitful outcomes and significantly advancing the progress of modern physics. In history, there is a fascinating tale about the mathematician Hilbert. Upon learning of Einstein’s initial concepts regarding the exploration of general relativity, Hilbert was able to deduce the correct field equation for general relativity using the PLA several days before Einstein did. This equation is now commonly referred to as the Einstein field equation (or the Einstein-Hilbert action) of general relativity. On the other hand, mathematician Noether combined this principle with symmetry to derive Noether’s theorem - the relationship between symmetry and conservation laws - which provides another cornerstone in physics. Therefore, the PLA plays a central role in physics as it can be used to derive almost all fundamental dynamic equations in physics.

The celebrated physicist Richard Feynman (1918-1988) was first introduced to the concept of PLA in high school by his teacher, and he was struck by its remarkable simplicity and elegance. His profound comprehension of the subject ultimately led to significant breakthroughs in his work. In 1942, while pursuing his PhD, Feynman introduced the path integral formulation of quantum mechanics using the PLA. This became the third formulation of quantum mechanics, succeeding Schrödinger’s wave mechanics and Heisenberg’s matrix mechanics. Feynman’s path integral formulation offers a succinct, sophisticated, and classically-inspired representation of quantum mechanics. The path integral formulation greatly promoted the development of modern quantum physics and is the cornerstone of many fields, including quantum field theory, quantum statistics, and quantum gravity. However, the scientific community has not yet been able to experimentally measure the propagator, which is a crucial physical quantity in the path integral formulation. This has kept the basic concept of the formulation in the theoretical stage. Furthermore, the lack of technology to measure propagation has prevented the experimental demonstration or validation of the PLA in quantum mechanics.

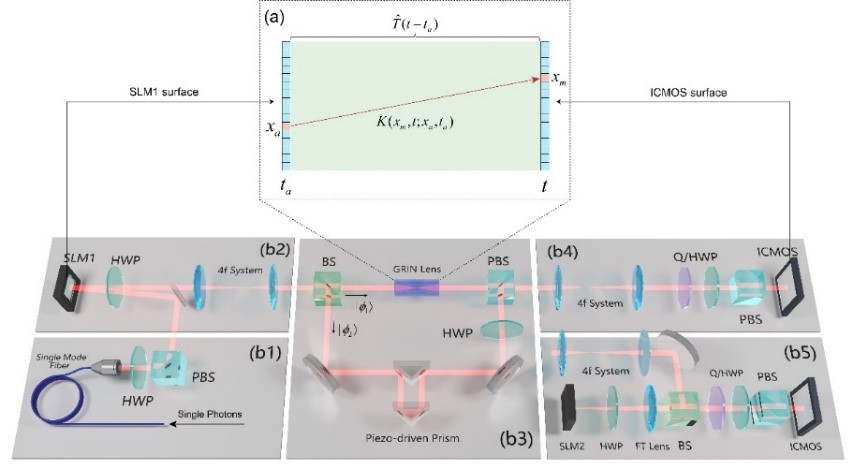
                                Figure 1

The main difficulty in measuring the propagator lies in the fact that it is a complex number and traditional quantum measurement techniques cannot directly measure it. Inspired by the method of directly measuring a wave function, the Yan-Zhu’s team has developed an experimentally feasible measurement scheme for the propagator. This scheme correlates the real and imaginary components of the propagator with observable quantities in the experiment, and then proceeds to reconstruct the propagator. Following this, the research team established and developed a quantum optics experimental system (Figure 1) based on this scheme. During the experiment, single photons were initially coupled with spatial and polarization modes, and then transmitted through a medium with gradient refractive indices for evolution. Finally, the spatial distribution of the photon was detected using a camera capable of detecting single photons. The real and imaginary parts of the propagator were then analyzed and reconstructed from the spatial distribution of the photons in various polarization states. The results of the experiment showed a highly consistent measurement of the propagator with the theoretical results calculated by Feynman’s path integral theory. Finally, the spatial distribution of the photon was detected using a camera capable of detecting single photons. The real and imaginary parts of the propagator were then analyzed and reconstructed from the spatial distribution of the photons in various polarization states. The results of the experiment showed a highly consistent measurement of the propagator with the theoretical results calculated by Feynman’s path integral theory.

   After successfully measuring the propagator, the research team further conducted research on verifying the PLA in quantum level through the propagator. Since the action is proportional to the phase factor of the propagator, analyzing the phase of the measured propagator and finding the extremum of the propagator phase through the PLA can determine the classical path of a single photon.  The results of this study provide valuable insights into the behavior of photons in different environments and can potentially lead to new developments in quantum optics and information processing.l.

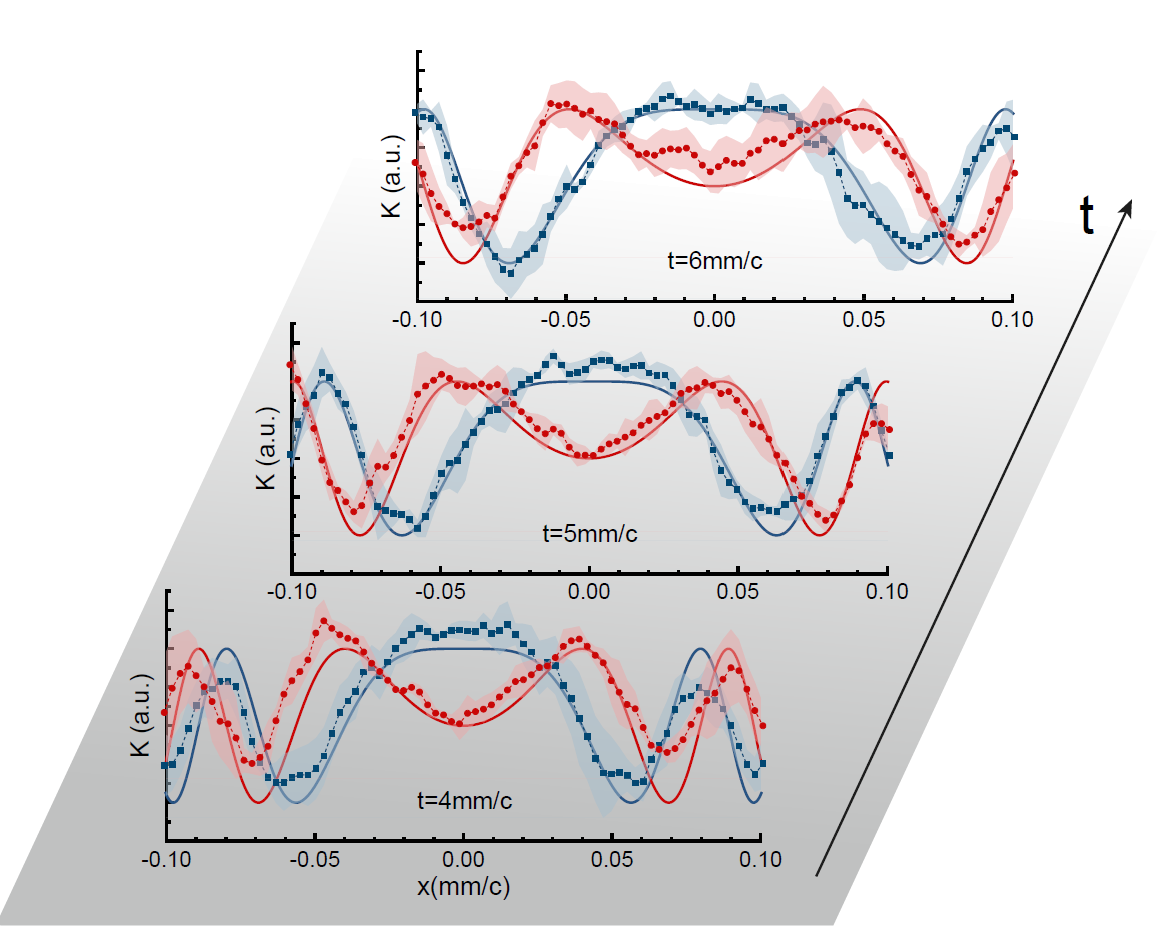
                          Figure 2

After successfully measuring the propagator, the research team further conducted research on verifying the PLA in quantum level through the propagator. Since the action is proportional to the phase factor of the propagator, analyzing the phase of the measured propagator and finding the extremum of the propagator phase through the PLA can determine the classical path of a single photon. After successfully measuring the propagator, the research team further conducted research on verifying the PLA in quantum level through the propagator. Since the action is proportional to the phase factor of the propagator, analyzing the phase of the measured propagator and finding the extremum of the propagator phase through the PLA can determine the classical path of a single photon. After analyzing a large amount of experimental data on the measured propagator, the research team successfully obtained the classical paths of a single photon in free space and in a harmonic potential (Figure 3), which agreed with the paths predicted by theory of path integral.

Quantum mechanics and classical mechanics are two fundamental branches of physics. The propagator is a crucial physical quantity in Feynman’s path integral approach to quantum mechanics. The first experimental measurement of the propagator holds immense scientific significance as it paves the way for experimental investigations into quantum phenomena associated with path integrals. The propagator is a crucial physical quantity in Feynman’s path integral approach to quantum mechanics. The first experimental measurement of the propagator holds immense scientific significance as it paves the way for experimental investigations into quantum phenomena associated with path integrals. Moreover, the PLA is a universal principle in physics, and demonstrating it in quantum systems can provide new insights for research in the fields of quantum-classical boundaries and the intersection of quantum mechanics and general relativity. The PLA has a long history and is a spiritual wealth derived from the joint efforts of many outstanding scientists. This experiment, for the first time, unveils its veil at the level of quantum experiments and reveals the scientific beauty and rational spirit behind it.

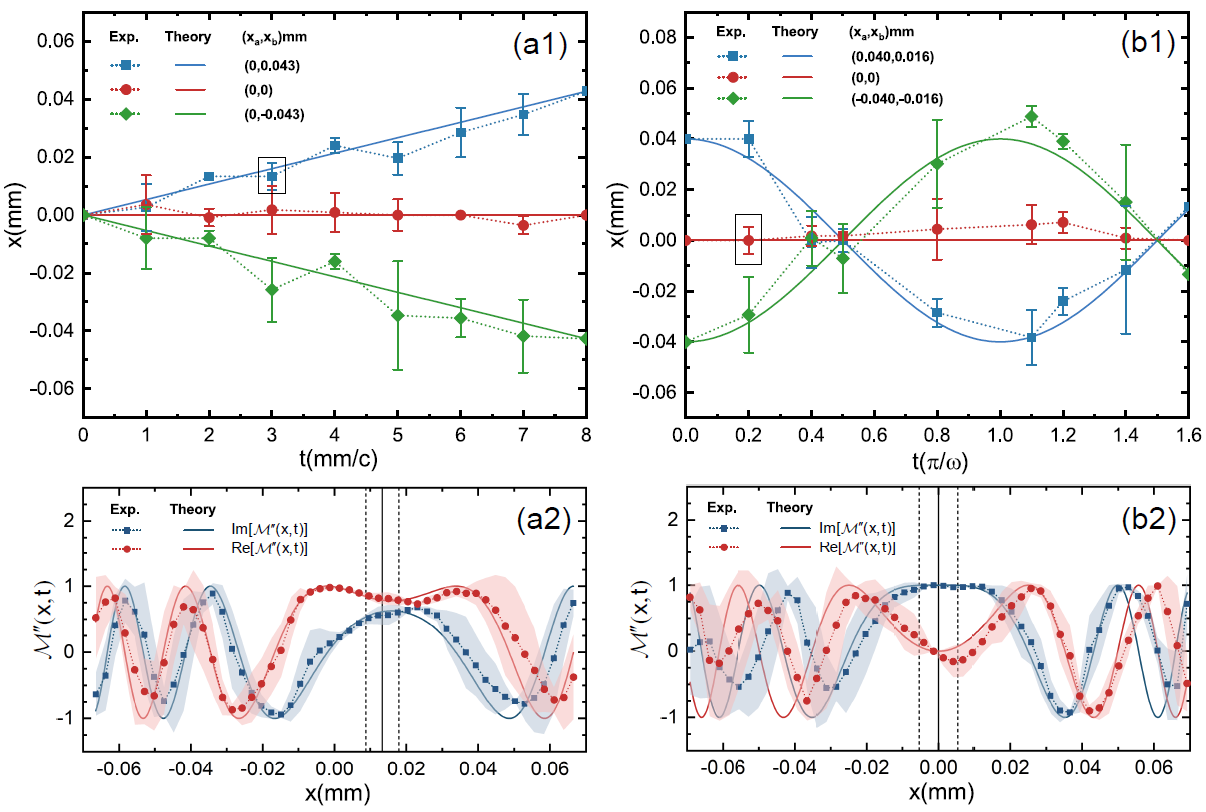
                               Figure 3