华南师范大学物理学院/学生成果 2022-05-23 09:25:29 来源:华南师范大学物理学院 点击: 收藏本文
我院郎利君副研究员指导的物理学拔尖基地本科生在非厄米拓扑领域发表最新的研究成果。相关成果以 “Gain/loss effects on spin-orbit coupled ultracold atoms in two-dimensional optical lattices” 为题,于2022年3月29日在线发表于物理学期刊《SCIENCE CHINA Physics, Mechanics & Astronomy》(中科院分区物理大类1区,2020年影响因子5.122),文章链接:http://engine.scichina.com/doi/10.1007/s11433-022-1898-7。我院2018级基地班本科生许志聪和2021级硕士生(原2017级基地班本科生)周子榆为文章的共同第一作者,2020级硕士研究生成恩宏及朱诗亮教授为共同作者,郎利君副研究员为通讯作者。
自旋-轨道耦合在超冷原子系统中的实现已经成为模拟和理解丰富多样的拓扑物态和拓扑相变的基石。近些年,非厄米物理的兴起拓展了大家对拓扑物相的理解。在自旋-轨道耦合系统中引入非厄米元素,不仅可以理解外界环境(比如测量或者干扰)对原物态(尤其是拓扑物态)的影响,还能探索由非厄米性导致的新奇物理现象。由于冷原子中成熟的单体原子损耗技术,实现和模拟非厄米的自旋-轨道耦合系统成为可能。本工作从理论上研究了增益/损耗对二维光晶格中自旋-轨道耦合超冷原子气体的影响,包括非厄米拓扑相图、节环(nodal loop)到异常环(exceptional loop)的劈裂、简并复能带的陈数计算以及体-边对应关系等。本研究加深了对非厄米拓扑物态的理解,有望促进对非厄米与自旋轨道耦合之间竞争的研究,且为在冷原子实验平台模拟相关现象提供理论依据。
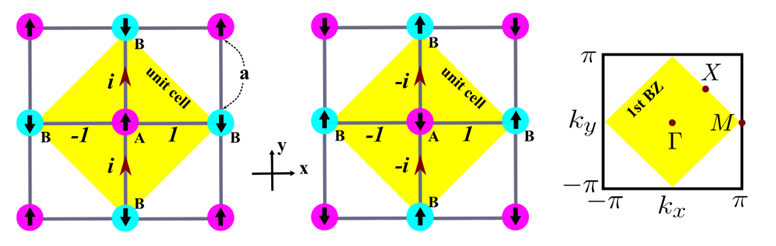
图1. 二维自旋轨道耦合光晶格的紧束缚模型及其布里渊区。
本文是基于冷原子实验已实现的二维自旋轨道耦合光晶格系统,其中的原子存在自旋上和下两种内态,晶格由A和B两种子格构成。在相应的紧束缚模型(图1左图和中图)中引入在位的自旋和子格依赖的增益/损耗项(可由相应的单体损耗技术实现),通过解析的方法计算得出此非厄米模型随增益/损耗强度变化的拓扑相图(图2),发现除了拓扑相和拓扑平庸相之外,还存在无能隙相。

图2. 非厄米拓扑相图,其中灰色部分为无能隙相。
此外还发现,当子格依赖的在位势仅由增益/损耗提供(即为纯虚势)时,原厄米情况下能量最低两能带间的节环(图3左图)会劈裂成异常环 —— 一种非厄米简并(图3右图),在环上原有的两个本征态合并成(coalesce)一个。
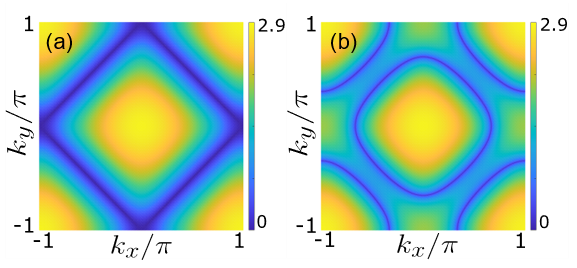
图3. (a)厄米情形下的节环。(b)非厄米情形下的例外环。
由于晶格具有棋盘的形状,其第一布里渊区为正方晶格的一半(图1右图),此模型具有四条复能带。为了计算具有非厄米简并的多条复能带的陈数,本文还发展了非厄米系统下的威尔逊圈方法,并发现只有利用左右矢定义的非厄米非阿贝尔贝里曲率才是协变的,不同于阿贝尔的情形。此方法能很好地计算出与其他能带存在复能隙时的多带陈数(图4)。
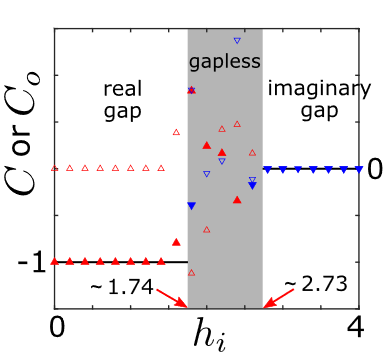
图4. 周期和开边界条件下的非厄米陈数。黑色实线为周期边界条件下由威尔逊圈方法计算的结果。三角形在开边界下计算的结果,红(蓝)色三角代表按能量实(虚)部排序,实(空)心三角代表陈数的实(虚)部。灰色区域为无能隙区。
为了检验此系统的体-边对应关系,本文还计算了开边界条件下的陈数。指出在该非厄米模型中,由于非厄米趋肤效应的缺失,传统的体边对应关系依然被保留了下来。不过,有趣的是,开边界下的手征边缘态的耗散行为依赖于开边界的选择,不同的边界(或缺陷)会导致其不同的动力学演化行为(图5)。
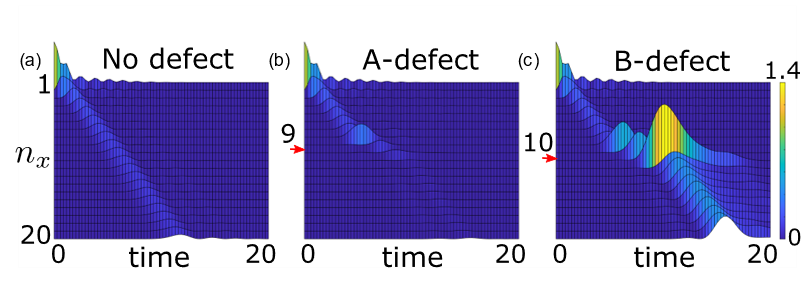
图5. 不同缺陷下手征边缘态的动力学演化。(a)边界无缺陷。(b)边界第9个格点处有A型缺陷。(c)边界第10个格点处有B型缺陷。
本研究得到国家自然科学基金、广东省基础与应用基础研究基金、广东省重点领域研发计划等项目的资助。
郎利君老师主要从事凝聚态物理中拓扑量子理论的相关研究,当前感兴趣的方向包括拓扑物态及相变、非厄米及非线性物理、强关联系统以及量子开放系统等。课题组常年招收本科生进行科研训练,并指导申报各类大学生科研竞赛项目。
拔尖基地学生简介

许志聪,2018级物理学基地班本科生,GPA 4.04/5.0,专业排名7/186,曾获“国家励志奖学金”(连续三年)、校综合二等奖学金、校学业表现奖学金、“院长年度荣誉学生”(连续三年)等荣誉,主持一项校级《大学生创新创业》项目并结题,即将成为郎利君老师课题组2022级硕士研究生。

周子榆,2017级物理学基地班本科生,GPA 3.62/5.0,曾获“国家励志奖学金”(连续两年)、广东省物理实验设计大赛二等奖、校“创新奖”等荣誉,参与一项省级《大学生创新创业》项目并结题,通过学校推免计划现为郎利君老师课题组2021级硕士研究生。