华南师范大学物理学院/科研成果 2023-12-06 10:42:00 来源:华南师范大学物理学院 点击: 收藏本文
我院广东省高等学校物质结构与相互作用基础研究卓越中心、广东省量子调控工程与材料重点实验室朱起忠副研究员,最近在二维超流方面取得重要研究进展,在理论上提出了二维半导体中可能存在的具有超越传统Berezinskii-Kosterlitz-Thouless范式的二维激子超流体。该研究成果以“Searching for Unconventional Superfluid in Excitons of Monolayer Semiconductors”为题,于12月5日在线发表在物理学国际顶级期刊 《Physical Review Letters》上(Phys. Rev. Lett. 131, 236004 (2023))。论文链接如下: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.236004
一个广为人知的事实是,根据Mermin-Wagner定理,传统二维均匀空间的玻色体系没有长程序,对应的玻色爱因斯坦凝聚的临界温度为零。但体系在低温下仍然存在超流,并且超流到正常态的转变温度非零,该相变由著名的Berezinskii-Kosterlitz-Thouless(BKT)理论描述。这是第一种由体系拓扑激发决定的相变,开辟了拓扑理论在物理学中广泛应用的时代,理论的提出者J. M. Kosterlitz和D. J. Thouless因此获得了2016年诺贝尔物理学奖。该理论广泛应用于一般的二维超流、超导等重要物理体系。寻找不能用该理论描述的二维超流是凝聚态物理中的重要问题,对于理解玻色爱因斯坦凝聚和超流等基本概念具有重要意义。
在这项工作中,研究组指出过渡金属硫化物中的层内激子可能形成超越BKT范式的非传统二维超流。他们首先通过考虑层内激子的能谷轨道耦合和能谷塞曼效应,得到在低能下具有线性色散的激子。基于目前报道的在层内激子流体方面的最新实验进展,研究组进一步系统研究了具有线性色散的激子形成的二维超流体的性质。他们发现与传统二维玻色体系不同,激子的玻色爱因斯坦凝聚转变温度变得非零,从而在二维均匀空间中激子可能存在真正的长程序。他们计算发现,考虑激子相互作用之后,凝聚转变温度进一步提高。并且,该激子超流的Bogoliubov激发谱与波矢之间呈根号的关系,这与传统的线性声子激发不同。另外与传统体系不同的是,涡旋激发能量具有额外的随体系尺寸的线性依赖项,这导致在大尺寸下,体系的超流相变偏离BKT理论,而与三维体系更接近。该体系的有限温相变包含两次相变,即先从激子玻色爱因斯坦凝聚相到超流相,再从超流相到正常相。理论预言的凝聚相和超流相可以通过在实验上测量激子复合发出的光子的关联函数来确定。该工作指出了二维均匀空间中具有线性色散的激子超流的奇特性质,对于在其它领域实现的具有类似色散的玻色体系也有启发意义。
我院硕士研究生陈伟为论文第一作者,朱起忠副研究员为论文通讯作者,华南师范大学为第一单位,另外参与该研究的还有香港大学的黄春炯博士。该工作得到了国家自然科学基金和广东省自然科学基金的支持。
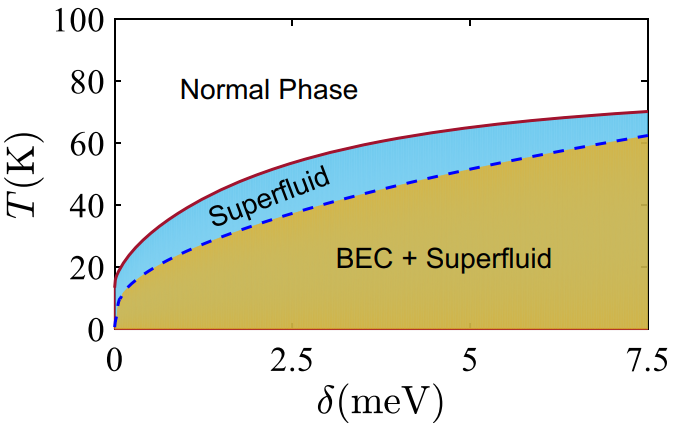
二维均匀空间具有线性色散的激子体系的有限温相图

论文首页信息